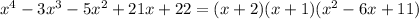Question

Factor
`f(x) = x^4 - 3x^3 - 5x^2 + 21x + 22` completely. Then sketch the graph with at least six points, including all roots and the y-intercept.

Answer 1

The rational root theorem suggests the following possible rational roots:

22, -22, 11, -11, 2, -2, 1, -1

(obtained by dividing all divisors of the constant term, 22, by the coefficient of the leading term, 1). Checking all of these possibilities, we happen to find that
`f(-2)=f(-1)=0`.

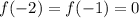By the polynomial remainder theorem (if
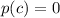`p(c)=0` for some polynomial
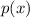`p(x)`, then
`x-c` divides
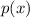`p(x)`), we then know that
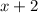`x+2` and
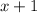`x+1` are factors.

Performing the division gives

`(x^4-3x^3-5x^2+21x+22)/((x+2)(x+1))=x^2-6x+11`

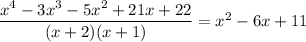
The remaining quadratic has discriminant

`\Delta=(-6)^2-4(1)(11)=-8<0`

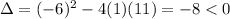
which means the remaining two terms are complex and the quadratic cannot be factored any further (over the real numbers). So

`x^4 - 3 x^3 - 5 x^2 + 21 x + 22=(x+2)(x+1)(x^2-6x+11)`