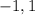Question

Locating zeros of polynomial functions

Answer 1

`a.\:\:-1,1`

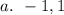
Explanation:

The given polynomial function is;

`f(x)=2x^4-x^3+x-2`

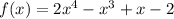
According to the rational roots theorem, the possible rational roots are

`\pm (1)/(2) ,\pm1,\pm2`

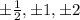
We now use the remainder theorem to obtain;

`f(1)=2(1)^4-(1)^3+(1)-2`

`f(1)=2-1+1-2`

`f(1)=0`

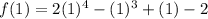
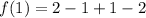
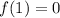
This implies that,
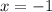`x=-1` is a zero.

Also,

`f(-1)=2(-1)^4-(-1)^3+(-1)-2`

`f(-1)=2+1-1-2`

`f(-1)=0`

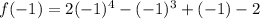
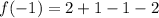
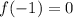
This means that,
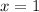`x=1` is also a zero.

`f((1)/(2))=-(7)/(4)`

`f(-(1)/(2))=-(7)/(4)`

`f(2)=2`

`f(-2)=2`

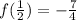
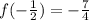
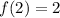
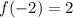
Hence the zeros are
`-1,1`