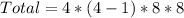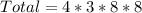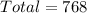Answer:
768 numbers
Explanation:
Given

Required
Number of digits between 0 ad 9999 that have one 1 and one 3
There are a total of 4 digits that make up any of the numbers in 0 to 9999 with the given condition
This can be represented as WXYZ
- Digit 1 can occupy any of the 4 positions
- Digit 3 can occupy any of the 4 - 1 positions
The remaining 8 digits will occupy the last 2 positions in the following ways:
- The first of the 8 digits can be selected from any of
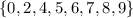 i.e. 8 ways
i.e. 8 ways
- The second can be selected from any of
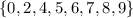 i.e. 8 ways
i.e. 8 ways
So, the total number of selection is: