Answer:
B) The function shown is
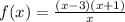
Explanation:
The given function is

This is an improper rational function because the degree of the numerator is greater than the degree of the denominator. This means the function has a slant asymptote and cannot have a horizontal asymptote.
The vetical asymptote is
 .
.
We factor the numerator to get;
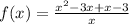
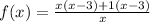
The function shown is the same as
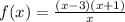
The zeros of this function are
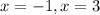
The correct answer is B