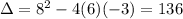1. The average rate of change of a function
 over an interval
over an interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) is given by the difference quotient
is given by the difference quotient
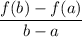
Here,

2. Complete the square to rewrite the quadratic in vertex form:
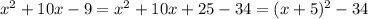
which indicates its vertex occurs at the point (-5, -34).
3. Check the discriminant. For a quadratic polynomial
 , the discriminant is
, the discriminant is
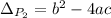
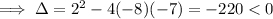
Because the discriminant is negative, there are two complex roots.
4. Same as before: