Answer: The correct option is (D) 108 units².
Step-by-step explanation: We are given to find the area of the special trapezoid ABCD in the figure, where
AB = 12 units, CD = 12 units and height, h = 9 units.
From the figure, we note that
AB = CD = 12 units and AB is parallel to CD.
So, one pair of opposite sides of the trapezoid are parallel and equal. That means, ABCD is a parallelogram.
The area of a parallelogram with base length b units and height h units is given by
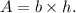
In the given parallelogram ABCD,
base, b = CD = 12 units
and
height, h = 9 units.
Therefore, the area of ABCD will be

Thus, the required area of the trapezoid is 108 units².
Option (D) is correct.