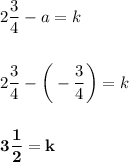Question

Please solve with steps.

the missing text on the photo:

The graph of y=a(x-h)^2 + k is shown alongside.
a) find the value of h.
b) find the values of a and k by solving simultaneous equations.

Answer 1

Answer: a) h = 2

b) a =
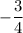`-(3)/(4)` k =
`\bold{3(1)/(2)}`

Explanation:

The vertex form of a quadratic equation is: y = a(x - h)² + k where

• a is the vertical stretch
• (h, k) is the vertex

The graph shows the axis of symmetry at x = 2, therefore, the x-coordinate of the vertex (h) is 2.

Two points are given:
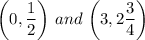`\bigg(0, (1)/(2)\bigg)\ and\ \bigg(3, 2 (3)/(4)\bigg)` . We can use these points to create two equations and then solve the system to find the a and k-values.

y = a(x - 2)² + k

`\bigg(0, (1)/(2)\bigg)\\\rightarrow (1)/(2)=a(0-2)^2+k\\\\\rightarrow (1)/(2)=4a+k\\\\\rightarrow (1)/(2)-4a=k\\\\\\\bigg(3, 2(3)/(4)\bigg)\\\rightarrow 2(3)/(4)=a(3-2)^2+k\\\\\rightarrow 2(3)/(4)=a+k\\\\\rightarrow 2(3)/(4)-a=k\\\\\\\\(1)/(2)-4a=2(3)/(4)-a\\\\(1)/(2)-2(3)/(4)=4a-a\\\\(2)/(4)-(11)/(4)=3a\\\\-(9)/(4)=3a\\\\-(9)/(4\cdot 3)=(3a)/(3)\\\\ \bold{-(3)/(4)=a}`

Solve for k:

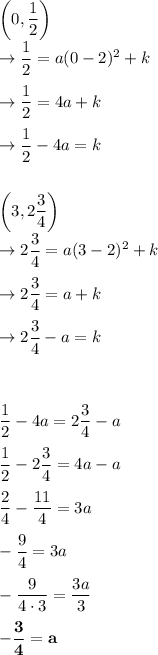
`2(3)/(4)-a=k\\\\\\2(3)/(4)-\bigg(-(3)/(4)\bigg)=k\\\\\\\bold{3(1)/(2)=k}`