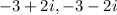Answer:
The zeros of given polynomial function
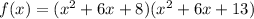 are -4 , -2
are -4 , -2
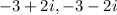
Explanation:
Given polynomial,
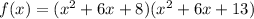
We have to find the zeros of the polynomial.
Consider the given polynomial,
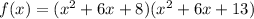
Zeros are the point where the value of function is equal to 0 that is
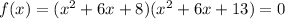
Using , zero product property ,
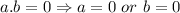
we have,
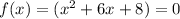 or
or
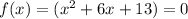
We solve it one by one,
consider
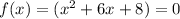
we solve the quadratic using middle term splitting method,
6x can be written as 4x + 2x ,
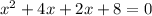
taking x common from first two term and 2 common from last two terms, we have,
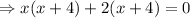
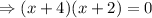
Again using zero product rule, we have,
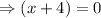 or
or
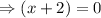
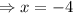 or
or
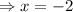
Now, consider the second quadratic equation
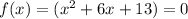
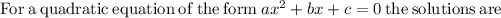
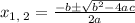
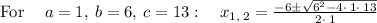
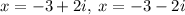
Thus, the zeros of given polynomial function
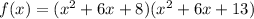 are -4 , -2
are -4 , -2