Question

You graph the function f(x)=-|x|-12 in the standard viewing window of –10 to 10. Will you be able to see the graph? Explain.

Answer 1

No, you will not see the graph.

When x is 0, y is –12, which is outside the viewing window.

Because the function has been reflected, it opens down.

From x = –10 to x =10, the y-values range from –22 to –12.

Explanation:

Answer 2

No, you will not be able to see the graph.

Explanation:

The given function is

`f(x)=-|x|-12`

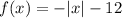
We need to check whether we will be able to see the graph in the standard viewing window of –10 to 10.

We know that absolute of modulus value is always greater than or equal to 0.

`|x|\geq 0`

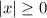
Multiply both sides by -1. If an inequality multiplied or divide by a negative number, then we need to change the sign of inequality.

`-|x|\leq 0`

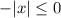
Subtract 12 from both sides.

`-|x|-12\leq 0-12`

`-|x|-12\leq -12`

`f(x)\leq -12`

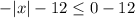
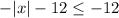
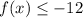
It means the value of function is always less than or equal to -12.

Range = (-∞,-12]

Standard viewing window means

X min = –10 and X max = 10

Y min = –10 and Y max = 10

Since the range of the function is (-∞,-12]. Therefore, you will not be able to see the graph.