Answer:
The scale factor is

Explanation:
The given line segment AB has vertices A(-3,4) and B(1,-2).
The image has vertices
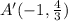 and
and
 .
.
The mapping for a dilation with scale factor
 centered at the origin is
centered at the origin is

Let the scale factor for the dilation be
 .
.
Then,
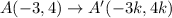
Comparing
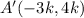 to
to
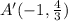 , we have
, we have

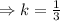
Or
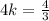
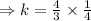 .
.
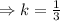 .
.
We could have also used the second point to obtain the same result.