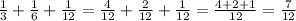Question

Use numbers from the box to find the equivalent fractions and the sum.​

Answer 1

`(1)/(3)+(1)/(6)+(1)/(12)=(4)/(12)+(2)/(12)+(1)/(12)=(7)/(12)`

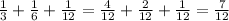
Explanation:

Given : Sum of fractions
`(1)/(3)+(1)/(6)+(1)/(12)`

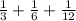
We have to first find an equivalent fractions then find the sum.

Consider the given fractions,

`(1)/(3)+(1)/(6)+(1)/(12)`

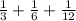
We first make the denominator of each fraction equal and we can do so by taking least common multiple of denominator of each fraction that is 3, 6, 12

Least common multiple is the smallest number that is divisible of all the given numbers.

Here , LCM (3, 6, 12 ) = 12

Thus, the equivalent fractions are,

`(1)/(3)*(4)/(4)=(4)/(12)\\\\(1)/(6)*(2)/(2)=(2)/(12)\\\\\\frac{1}{12}=(1)/(12)`

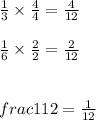
and sum of fraction is :
`(1)/(3)+(1)/(6)+(1)/(12)=(4)/(12)+(2)/(12)+(1)/(12)=(4+2+1)/(12)=(7)/(12)`