Question

Write the equation of the line parallel to 3x-y=7 that passes through point (-5, -3)

Answer 1

`\boxed{y=3x+12}`

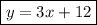
Explanation:

In this problem we know the equation of a line, which is:

`3x-y=7`

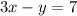
We also can write this equation as:

`y=3x-7`

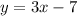
This line has a slope
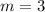`m=3` which is also the slope of the line we are looking for because they're parallel. We also have a point
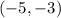`(-5,-3)`. Therefore, we can write this equation as follows:

`y-y_(0)=m(x-x_(0)) \\ \\ y-(-3)=3(x-(-5)) \\ \\ y+3=3(x+5) \\ \\ y+3=3x+15 \\ \\ \boxed{y=3x+12}`

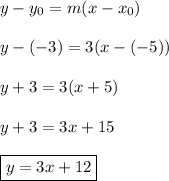
From the figures below, the line in red is
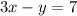`3x-y=7` while the line in blue is
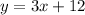`y=3x+12` and this line passes through the point (-5, -3)!

Answer 2

The equation of the line is y =3x+12

Explanation:

The first step is to rewrite the equation of the line in the slope-intercept form in order to identify the slope of the line. The re-written equation is; y = 3x-7. This implies that the slope of the line is 3. Since the two lines will be parallel they will be having equal slopes of 3. The slope-intercept form of the equation of this line will be; y =3x+c. Since the line passes through (-5, -3), substitute x with -5 and y with -3 to solve for c; -3 =3(-5)+c. Then c =12 and the equation of the line becomes; y =3x+12