Answer:
b) Shift the graph of y = x2 down 12 units.
Explanation:
Graphs
The graph of the function
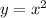
can be found by giving the variable x some values and calculating the values of y as follows:
For x=-2,
 . Point (-2,4)
. Point (-2,4)
For x=-1,
 . Point (-1,1)
. Point (-1,1)
For x=0,
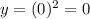 . Point (0,0)
. Point (0,0)
For x=1,
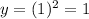 . Point (1,1)
. Point (1,1)
For x=2,
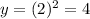 . Point (2,4)
. Point (2,4)
The graph of
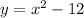
Can be similarly found:
For x=-2,
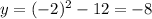 . Point (-2,-8)
. Point (-2,-8)
For x=-1,
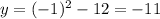 . Point (-1,-11)
. Point (-1,-11)
For x=0,
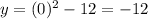 . Point (0,-12)
. Point (0,-12)
For x=1,
 . Point (1,-11)
. Point (1,-11)
For x=2,
 . Point (2,-8)
. Point (2,-8)
The graphs are shown in the attached image. It can be clearly seen that the second graph (in blue) is shifted down 12 units with respect to the red graph. Answer:
b) Shift the graph of y = x2 down 12 units.