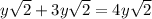Question

Perform the indicated operation. Assume all variables represent non-negative real numbers


`\sqrt{2y^(2) } +y√(18)`

Answer 1

`y√(2) + 3y√(2) = 4y√(2)`

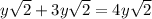
Explanation:

To add or subtract radicals, you need to simplify the radicals and then add the radicals

`√(2y^2) + y√(18)`

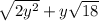
First simplify
`√(2y^2)`

`√(2y^2)`

`√(2y^2) = √(2) \ √(y^2)`

`√(2) \ √(y^2)`

`√(y^2) = y`

`√(2) \ y`

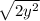
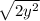
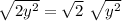
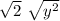
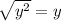
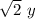
OR

`y√(2)`

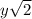
Second simplify
`√(18)`

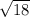
To simplify
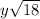`y√(18)` you need to find two radicals that =
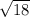`√(18)` when you multiply them. One radical needs to be a perfect square and the other needs to be a non perfect square.

`√(18)`

`√(9) * √(2) = √(18)`

`√(9) * √(2)}`

`√(9) √(2)}`

`3 √(2)}`

`3 y√(2)}`

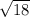
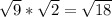
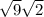
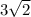
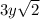
Now put it all together

`y√(2) + 3y√(2) = 4y√(2)`