Question

Please i need an answer urgently. Sum of 3 terms are 252, first term is 192. Find common ratio

Answer 1

`r=(1)/(4)\\\\r=-(5)/(4)`

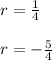
Explanation:

Geometric Sequences

The geometric sequence is given as:

`a_1, a_1r, a_1r^2, a_1r^3,..., a_1r^(n-1)`

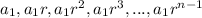
Where n is the number of the term, n≥1, and r is the common ratio.

The sum of n terms of the geometric sequence is given by:

`\displaystyle S_n=a_1(r^n-1)/(r-1)`

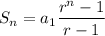
We are given: S3=252, a1=192, thus substuting:

`\displaystyle 252=192(r^3-1)/(r-1)`

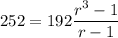
Dividing by 12:

`\displaystyle 21=16(r^3-1)/(r-1)`

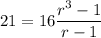
Recall that:

`r^3-1=(r-1)(r^2+r+1)`

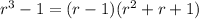
Substituting:

`\displaystyle 21=16((r-1)(r^2+r+1))/(r-1)`

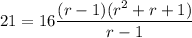
Simplifying:

`21=16(r^2+r+1)=16r^2+16r+16`

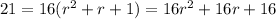
Rearranging:

`16r^2+16r+16-21=0`

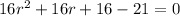
16r^2+16r-5=0

Rewriting:

`16r^2-4r+20r-5=0`

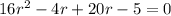
Factoring:

`4r(4r-1)+5(4r-1)=0`

`(4r-1)(4r+5)=0`

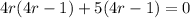
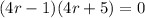
Solving:

`r=(1)/(4)\\\\r=-(5)/(4)`

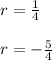
Both solutions are valid