Answer:
A.) (7t³ + 2k^4)(7t³ - 2k^4)
Explanation:
This is what we call a conjugate binomial which is two binomials with similar terms but with one of those terms with different signs, this shows a result of the first term squared minus the second term squared.
The formula for conjugate binomials are:
(a+b)(a-b)=
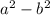
In this case the multiplication of
(7t³ +
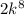 )(7t³ -
)(7t³ -
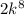 )= 49
)= 49
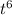 + 14
+ 14
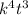 - 14
- 14
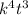 -
-
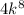
After substracting the second and the third term you are left with:
