Answer:
The solution of the system of equations will be:

Explanation:
Given the system of equation

Arrange equation variables for elimination
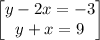
so
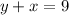

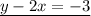
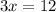
so the system of equations becomes
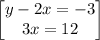
solve 3x=12 for x
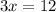
Divide both sides by 3
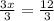
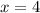
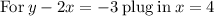
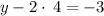
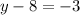
Add 8 to both sides

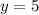
Thus, the solution of the system of equations will be:
