Question

Given the functions

F(x) = 1/x-4 + 3 and G (x) = 1/x+1 + 6
Which statement describes the transformation of the graph of function F onto the graph of function G?
A- the graph shifts 5 units right and 3 units down
B- the graph shifts 5 units left and 3 units up
C- the graph shifts 3 units right and 5 units down
D- the graph shifts 3 units left and 5 units up.

Answer 1

Option B.

Explanation:

The first transformation we can apply is to do:

F(x) +3

As

`F(x) = (1)/(x-4) + 3`

So

`F(x) +3 = (1)/(x-4) + 6`.

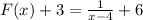This operation moves the function upwards by 3 units.

The second transformation is to make F(x + 5)

`F(x+5) = (1)/((x+5)-4) + 6\\\\F(x+5) = (1)/((x+1)) + 6`

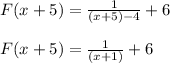
This transformation moves the function 5 units to the left.

Note that now
`F(x + 5) +3 = G(x).`

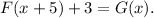
The results of these transformations was an upward displacement of 3 units and one to the left of 5 units.

Finally the answer is option B

B- the graph shifts 5 units left and 3 units up

Answer 2

B- the graph shifts 5 units left and 3 units up

Explanation:

The function F(x) = 1/x-4 + 3 can be transformed to G (x) = 1/x+1 + 6,

The transformation can be determined by comparing the two functions;

Such that; (1/x+1 + 6) - (1/x-4 + 3) we get; +5 , +3

Which means; the function F(x) = 1/x-4 + 3 can be transformed to G (x) = 1/x+1 + 6; by shifting the graph 5 units left and 3 units up, since 5 is positive (left) and 3 is positive (up).