Answer:
Choice C is the correct answer
Explanation:
The first step is to factorize the numerator;
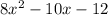
We need to determine two numbers such that their sum is -10 and their product 8(-12) = -96. The two numbers by trial and error are -16 and 6. Consequently, we substitute the middle term in the expression by these two numbers;
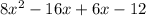
Upon simplification this becomes;
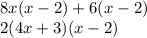
Dividing by the denominator the common terms 4x+3 cancel each other and the quotient thus becomes;
2x-4