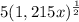Question

Which is equivalent to 5√1,215x

Answer 1

Answer with explanation

The expression whose equivalent expression we have to find is:

`\Rightarrow 5 √(1215 x)\\\\\text{Following are the equivalent expression}\\\\1.\rightarrow 5 √(243 * 5* x)\\\\2.\rightarrow 5 *√(3* 3* 3* 3* 3* 5 * x)\\\\3.\rightarrow 5 * 3* 3 * √(15 x)\\\\ 4.\rightarrow 45 √(15 x)\\\\5. \rightarrow 45 * (15)^{(1)/(2)} * x^{(1)/(2)`

Answer 2

Answer:
`5(1,215x)^{(1)/(2)}`

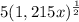
Step-by-step explanation:}

To solve this problem you can apply the proccedure shown below:

1. By definition, you have that:

`\sqrt[n]{a}=a^{{(1)/(n)}`

2. Therefore, keeping the above on mind, you can find an equivalent expression of
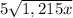`5√(1,215x)` as following:

`5√(1,215x)=5(1,215x)^{(1)/(2)}`

3. Then, an equivalent expression is:

`5(1,215x)^{(1)/(2)}`