Question

A country’s population in 1994 was 32 million estimate the population in 2003

Answer 1

36 million is the answer.

Explanation:

In the question given parameters are population in 1995 = 32 million

Population in 1997 = 34 million

Exponential growth formula is
`P = Ae^(kt)`

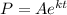
And we have to find out the population in 2003.

Here From this formula initial population in 1995
`P=Ae^(k* 0)=32`

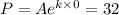
Or P = A = 32 million

Now population in 1997

`P=32e^(k* 2)=34`

`e^(k* 2)=34/32=17/16`

`log(e^(2k))=log((17)/(16))`

`2k=log17-log16`

`2k=0.0263`

`k=0.0131`

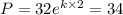
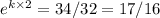
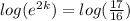
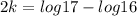
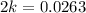
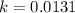
Now Population in 2003

`P=32e^(.0131* 8)=32e^(0.105)`

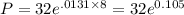
P = 32×1.11 = 35.54 million ≅ 36 million