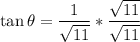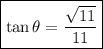Question

What is tan theta when csc theta =2 sqrt 3?

Not really understanding how this works. If possible can someone explain step by step?

Answer 1

`\displaystyle \tan\theta=(√(11))/(11)`

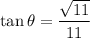
Explanation:

Trigonometric Identities

If the trigonometric function value of an angle is given, we can find the rest of the trigonometric values of the angle by using one or more of the fundamental identities.

To solve this problem, we need to use the following identities:

`\displaystyle \cot^2\theta=\csc^2\theta-1`

`\displaystyle \tan\theta=(1)/(\cot\theta)`

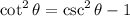
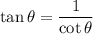
Since we are given:

`\displaystyle \csc\theta=2√(3)`

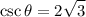
And the angle is in the first quadrant, calculate the cotangent:

`\displaystyle \cot^2\theta=(2√(3))^2-1`

`\displaystyle \cot^2\theta=4*3-1=11`

`\displaystyle \cot\theta=√(11)`

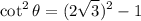
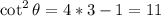
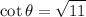
The tangent is:

`\displaystyle \tan\theta=(1)/(√(11))`

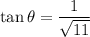
Rationalizing the denominator:

`\displaystyle \tan\theta=(1)/(√(11))*(√(11))/(√(11))`

`\boxed{\displaystyle \tan\theta=(√(11))/(11)}`