Answer:
The correct option is 4. The value of R² is 1.000.
Explanation:
The table lists the distance d (in ft) above the ground for an object dropped in a vacuum from a height of 500 feet. The time t (in sec) is the time after the object has been released.
The general form of quadratic regression is

Use technology, we get
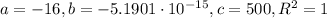
The required quadratic regression is
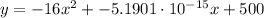
The value of R² is 1.000. Therefore the correct option is 4.