Question

Find a recursive formula for the sequence: 1, -1,-7,-25

Answer 1

Check the forward differences:

-1 - 1 = -2

-7 - (-1) = -6

-25 - (-7) = -18

Notice how the differences appear to follow a geometric progression with common ratio 3. So if
`a_n` denotes the
`n`th term in the given sequence, we seem to have

`a_2-a_1=-2\cdot3^0`

`a_3-a_2=-2\cdot3^1`

`a_4-a_3=-2\cdot3^2`

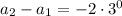
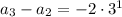
so that the general pattern for
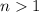`n>1` would be

`a_n-a_(n-1)=-2\cdot3^(n-2)`

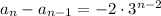
Then the sequence is given recursively by

`a_n=\begin{cases}1&\text{for }n=1\\a_(n-1)-2\cdot3^(n-2)&\text{for }n>1\end{cases}`

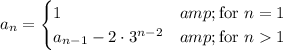
The first 10 terms in the sequence would be

1, -1, -7, -25, -79, -241, -727, -2185, -6559, -19681