I'm assuming
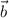 is the vector field I've suggested in my comment,
is the vector field I've suggested in my comment,
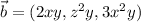
Parameterize the given surface - call it
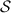 - by
- by
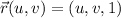
with
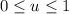 and
and
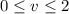 . The flux is given by the surface integral
. The flux is given by the surface integral

where the surface element is

(or use
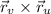 , depending on the orientation of the surface)
, depending on the orientation of the surface)
We have
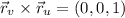
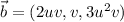
so the surface integral reduces to
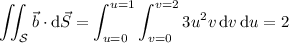
(or possibly -2, again depending on the orientation of
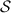 )
)