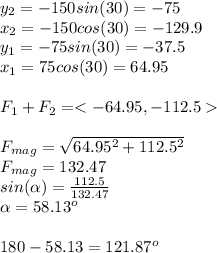Answer:
1.
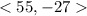
2.
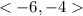
3.
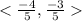
4.
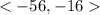
5.
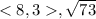
6.132.47 pounds at 121.87°
Explanation:
Question 1
Find 4u and 3v seperately by simply multiplying the constant with each part of the vector:
4u = <28,-12>
3v = <-27,15>
Then, 4u - 3v = <55,-27>
Question 2
Add the two vectors together:
u + v = <-3-3,-5+1>
u + v = <-6,-4>
Question 3
Consider vector u as a triangle of which the short sides have lengths of 3 and 4. Using Pythagoras, the length of the vector(the hypotenuse of the triangle) can be calculated as 5. A unit vector has a length of 1 along its hypotenuse. To convert the vector to a unit vector, everything has to be divided by five.
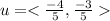
Question 4
Multiply both components of the vector by 8:
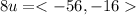
Question 5
Vector PQ has two end points, P=(5,9) and Q=(13,12)
The vector is basically a line drawn between the two points
Thus, the lengths in both the x and y direction can be found by subtracting one from the other:
PQ=<13-5,12-9>
PQ=<8,3>
The magnitude is considered as the hypotenuse of a traingle with short sides of 8 and 3. Using Pythagoras the magnitude can be solved:
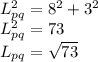
Question 6
See attached image.