Question

Find the sum of the first 12 terms of the sequence. 1, -4, -9, -14, . . . (2 points)

Answer 1

sum of the first 12 terms of the sequence. 1, -4, -9, -14, . . = -318

Explanation:

The given AP is,

1, -4, -9, -14, . . .

first term a = 1,

common difference d = -4 - 1 = -5

number of terms n = 12

Equation:

Sum of n terms of AP, S₁₂ = n/2[2a + (n - 1)d]

S₁₂ = 12/2[(2*1) + (12 - 1)*(-5)]

S₁₂ = 6[2 + (11*(-5))]

S₁₂ = 6[2 - 55] = 6*(-53) = -318

Therefore sum of the first 12 terms of the sequence. 1, -4, -9, -14, . . = -318

Answer 2

The sum of first 12 terms of the sequence. 1, -4, -9, -14, . . is -318.

Explanation:

Given sequence 1, -4, -9, -14, . . .

We have to find the sum of first 12 terms of the sequence. 1, -4, -9, -14, . .

Consider the given sequence 1, -4, -9, -14, . . .

`a_1=1 ,a_2=-4,a_3=-9`

First calculate the common difference (d)

`a_2-a_1=-4-1=-5\\a_3-a_2=-9+4=-5`

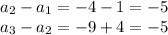
Thus, common difference is -5

We know sum of terms in an Arithmetic progression is given by,

`S_n=(n)/(2)(2a+(n-1)d)`

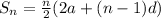
where n is number of terms ,

a = first term

d = common difference

Here, n = 12 , a= 1 , d = -5

`S_(12)=(12)/(2)(2(1)+(12-1)(-5))`

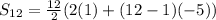
Solving , we get,

`S_(12)=6(2+11(-5))`

`S_(12)=6(2-55)`

`S_(12)=6(-53)`

`S_(12)=-318`

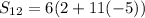
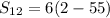
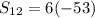
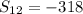
Thus, the sum of first 12 terms of the sequence. 1, -4, -9, -14, . . is -318.