Question

Which of the following is an accurate statement about vectors?

The magnitude of a vector may be positive even if all of its components are negative.

The magnitude of a vector can be zero even if one of its components is not zero.

If two vectors have unequal magnitudes, it is possible that their vector sum is zero.

Rotating a vector about an axis passing through the tip of the vector does not change the vector.

It is possible to add a scalar quantity to a vector.

Answer 1

Answer: The magnitude of a vector may be positive even if all of its components are negative.

Step-by-step explanation:

A vector has both magnitude and direction unlike a scalar which has magnitude only.

A vector can be written in terms of its components:

`\vec{a} = a_x\hat{i}+a_y\hat{j}+a_z\hat{k}`

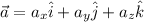
The magnitude of the vector is given by:

`|a| =√(a_x^2+a_y^2+a_z^2)`

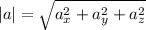
Thus, even if all the components of the vector are negative, the vector can have a positive magnitude.

The magnitude would be non-zero if one of its components is non-zero.

some of two vectors involves summation of magnitudes of of the vector components in the same direction. Two vectors having unequal magnitudes cannot have vector sum zero.

Rotating a vector about an axis passing through the tip of the vector changes the vector as the direction changes.

A scalar quantity cannot be added to a vector as it lacks the direction.

Answer 2

Answer;

The magnitude of a vector may be positive even if all of its components are negative.

Explanation;

• Two vectors are equal if they have the same magnitude and the same direction. If two vectors have the same magnitude (size) and the same direction, then we call them equal to each other.
• A negative vector is a vector that has the opposite direction to the reference positive direction.
• When vectors are added, we take into account both their magnitudes and directions.