Question

I need physics help!!

Answer 1

Answer: magnitude = 5 and angle = 160°

Step-by-step explanation:

A vector has magnitude 5 and angle -20°

A vector can be written in terms of its components as :

`\vec{A}=A_x\hat{i}+A_y\hat j \\ \Rightarrow \vec A = A cos\theta \hat i+A sin\theta \hat j`

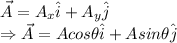
using trigonometry identity:

sin θ = -sin ( 180 + θ )

cos θ = - cos (180 + θ)

Thus, we can write the same vector as:

`\vec A = -A cos(180+\theta) \hat i+(-A) sin(180+\theta) \hat j`

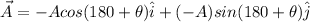
Magnitude
`|A|=√((-A)^2+(-A)^2) = A = 5`

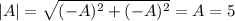
Thus, the magnitude would be A = 5 and angle = 180+θ= 180-20 = 160°