Question

If rectangle ABCD, defined by the coordinates A(0, 0), B(0, -4), C(-2, -4), D(-2, 0), is dilated by a scale factor of 2, with resulting vertex A' at (2, 4), what is the center of the dilation? A) (0, 0) Eliminate B) (2, 4) C) (0, -4) D) (-2, -4)

Answer 1

D) (-2, -4).

Explanation:

Let
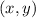`(x, y)` be the center of dilation. Imagine that
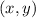`(x, y)` is the center of origin of a new Cartesian Plane. What would the coordinates of point A and A' on the new plane?

• A:
  `(0 - x, 0 - y)` ⇒
  `(-x, -y)`.
• A':
  `(2 - x, 4 - y)`.

Dilating
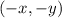`(-x, -y)` about the "origin" of the new plane by a factor of two will give the point
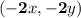`(-{\bf 2}x, -{\bf 2}y)`, also on the new plane.

For coordinates of A' on the original plane,

`(-{2}x, -{2}y) = (2 - x, 4 - y)`.

As a result,

`\left \{ \begin{array}{l}-2x = 2 - x\\-2 y = 4 - y\end{array}`.

`\left \{ \begin{array}{l}-x = 2\\- y = 4\end{array}`.

`\left \{ \begin{array}{l}x = -2\\y = -4\end{array}`.

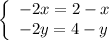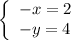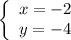In other words,
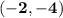`{\bf (-2, -4)}` is the center of dilation.