Answer:
The distance from A to B is 736.2 to the nearest tenth foot
Explanation:
In ΔCAB
∵ m∠CAD = 30° ⇒ exterior angle of Δ at vertex A
∴ m∠CAD = m∠ACB + m∠ABC
∵ m∠ABC = 20°
∴ m∠ACB = 30° - 20° = 10°
We will use the sin rule to find the distance AB
∵
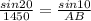
∴
 ≅ 736.2 to the nearest tenth foot
≅ 736.2 to the nearest tenth foot