Question

For security, a credit card number is coded in the following way, so that it can be sent as a message. Subtract each digit from 9.

1. Code the credit card number 3201 2342 3458 0931.

2. A coded credit card number is 2341 0135 7923 0133. What is the original credit card number?

3. Find f(x) if x represents a single input digit. What is the domain
of f(x)?

4. Find f-1(x). What is the domain of f-1(x)?

Answer 1

1. 6798 7657 6541 9068.

2. 7658 9864 2076 9866.

3.
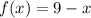`f(x)=9-x` and domain of f(x) is {0,1,2,3,4,5,6,7,8,9}.

4.
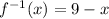`f^(-1)(x)=9-x` and domain of f⁻¹(x) is {0,1,2,3,4,5,6,7,8,9}.

We are given that,

The coding method for the card number is 'Subtract each digit from 9'.

So, we have,

Part 1: The number given is 3201 2342 3458 0931.

So, after subtracting each digit from 9, we have,

The coded number is 6798 7657 6541 9068.

Part 2: The coded number given is 2341 0135 7923 0133.

To find the original number, we will subtract the digits from 9.

The original number is 7658 9864 2076 9866.

Part 3: We have f(x), where x represents the single input digit.

That is, 'x' can have values from {0,1,2,3,4,5,6,7,8,9}.

As, the coded output is the number subtracted from 9.

We get, the function is
`f(x)=9-x`.

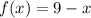So, the domain of f(x) is {0,1,2,3,4,5,6,7,8,9}.

Part 4: We need to find the inverse function.

So, we have,
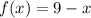`f(x)=9-x` i.e.
`x=9-f(x)`.

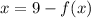Thus, the inverse function is
`f^(-1)(x)=9-x`

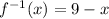
Since, the range of f(x) is the domain of f⁻¹(x).

The domain of f⁻¹(x) is {0,1,2,3,4,5,6,7,8,9}.