Answer:
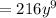
Explanation:
the expression is:
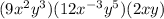
the first step is to multiply all the coefficients:
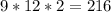
and as for the variables, to multiply them we must add the exponents, that is, the result for x will be:
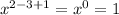
so there will be no x in our result.
adding the exponents for the y variable:
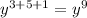
The result is the multiplied coefficients and the variables after we add the exponents they in the original expression:
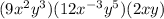
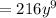
which is option B