Answer:
A. -1, multiplicity 1; 0, multiplicity 1; 3, multiplicity 1.
Explanation:
Let
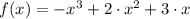 , to determine its roots and multiplicities we proceed to factorize the polynomial:
, to determine its roots and multiplicities we proceed to factorize the polynomial:
1)
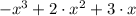 Given
Given
2)
 Distributive property
Distributive property
3)
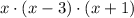 Quadratic formula/Result
Quadratic formula/Result
The roots and multiplicities of
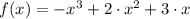 are:
are:
0 (multiplicity 1)
3 (multiplicity 1)
-1 (multiplicity 1)
Therefore, the correct answer is A.