Answer: 80°
Explanation:
Since, If two secants intersect outside the circle, then the measure of the angle formed is one half of the difference of the measures of the intercepted arcs.
In the given diagram,
Chord VS and chord UT are intersecting externally,
Also, ∠SPT is the angle formed by the intersection of these chords.
Thus, by the above property,
![(1)/(2)[m(\widehat{VU})-m(\widehat{ST})]=m\angle SPT](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yv8p4eac2qxi4lfe8azfgocczdd64xsbnc.png)
![\implies (1)/(2)[m(\widehat{VU}) - 20^(\circ)]= 30^(\circ)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1tl4kkzljtsuyygkto15d22w7mza10l366.png)
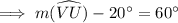
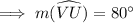
⇒ Measurement of the arc VU= 80°.