Answer:
a) The height of the building is 12 metres.
b) The ball will take 6 seconds to hit the ground.
c) The maximum height of the ball is 16 metres and occurs 2 seconds after launch.
d) The ball have a height of 7 meters above the ground 5 seconds after launch.
Explanation:
a) The roof of the building is represented by the initial height of the ball according to the function. If we know that
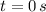 , the height of the building, measured in metres, is:
, the height of the building, measured in metres, is:
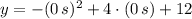
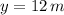
The height of the building is 12 metres.
b) Let equalise the given polynomial and solve for
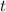 to determine the time taken for the ball to hit the ground:
to determine the time taken for the ball to hit the ground:
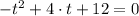 (1)
(1)
By the Quadratic Formula, we find the following solutions:
 and
and
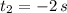
Since time is a positive variable, then the only solution that is physically reasonable is:
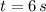
The ball will take 6 seconds to hit the ground.
c) The maximum height of the ball occurs when speed is equal to zero. First, we differentiate the function and equalise to zero:
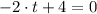 (2)
(2)
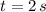
Lastly, we evaluate the function at given time:
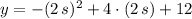
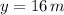
The maximum height of the ball is 16 metres and occurs 2 seconds after launch.
d) We equalise the height formula to seven and solve the resulting polynomial:
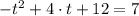
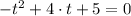 (3)
(3)
By the Quadratic Formula, we get the following solutions:
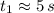 and
and
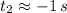
The only solution that is physically reasonable is
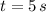 .
.
The ball have a height of 7 meters above the ground 5 seconds after launch.