Question

Circle A is shown with a central angle marked 42 degrees and the radius marked 8 inches.

Which of the following could be used to calculate the area of the sector in the circle shown above?

π(8in)42 over 360
π(42in)28 over 360
π(42in)8 over 360
π(8in)2 42 over 360 π(8in)2 42 over 360

Answer 1

D

Explanation:

Answer 2

D.
`\pi (8in)^(2)* (42)/(360)`

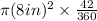
Explanation:

We are given that,

Radius of the circle = 8 inches

Central angle of the circle = 42°

As, we know,

Area of a sector of a circle =
`\pi r^(2)* (\theta)/(360)`

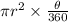
So, substituting the values, we get,

Area of a sector the circle =
`\pi 8^(2)* (42)/(360)`

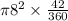
Thus, option D i.e.
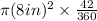`\pi (8in)^(2)* (42)/(360)` can be used to find the area of the sector.