Question

What is the solution of x^2-1/x^2+5x+4< or equal to 0

Answer 1

there is not a solution

Answer 2

(-4,-1) U (-1,1]

Explanation:

x^2-1/x^2+5x+4< or equal to 0

`(x^2-1)/(x^2+5x+4) \leq 0`

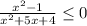
LEts factor top and bottom

`x^2+5x+4= (x+4)(x+1)`

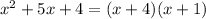
Now we factor x^2-1 using
`a^2-b^2=(a+b)(a-b)`

`x^2-1^2=(x+1)(x-1)`

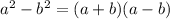
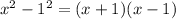
now we find the x values that makes the denominator 0

`(x+4)(x+1)=0`

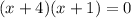
x+4=0, x=-4

x+1=0, x=-1

`((x+1)(x-1) )/((x+4)(x+1)) =0`

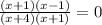
multiply the denominator on both sides

cancel out x+1 at the top and bottom

x-1 =0, x=1

We got 3 x values

x=-4, -1, 1

using the x values we make 4 intervals

(-∞, -4), (-4,-1) (-1,1] and [1,∞)

LEts pick a random number from each interval and check with the inequality

(-∞, -4) pick -5

`((-5)^2-1)/((-5)^2+5(-5)+4) \leq 0`

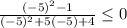
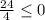`(24)/(4) \leq 0` false

(-4,-1) pick -3

`((-3)^2-1)/((-3)^2+5(-3)+4) \leq 0`

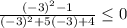
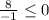`(8)/(-1) \leq 0` True

(-1,1] pick 0

`((0)^2-1)/((0)^2+5(0)+4) \leq 0`

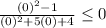
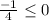`(-1)/(4) \leq 0` True

[1,∞) pick -2

`((2)^2-1)/((2)^2+5(2)+4) \leq 0`

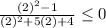
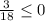`(3)/(18) \leq 0` false

solution are the intervals that satisfies our inequality

(-4,-1) U (-1,1]