Question

Find the center of the circle that can be circumscribed about EFG with E(4,4) F(4,2) G(8,2)

Answer 1

The center of the circle is (6 , 3)

Explanation:

∵ The vertices of Δ EFG are E (4 , 4) , F (4 , 2) , G (8 , 2)

∵ The x-coordinates of E and E are equal ∴ EF is vertical

∵ The y-coordinates of F and G are equal ∴ FG is horizontal

∴ m∠EFG = 90°

∵ The circle is circumscribed about Δ EFG

∴ E , F , G lie on the circle

∵ m∠F = 90°

∴ EG is the diameter of the circle

∴ The center of the circle is the mid-point of EG

∵ The mid-point of EG is
`((4+8)/(2),(4+2)/(2))=(6,3)`

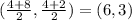
∴ The center of the circle is (6 , 3)