Answer:
Explanation:
Given that the radius of a bubble increases by 4%.
Let r be the radius of the spherical bubble, so the new radius of the sphere
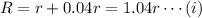
(a) Surface area of the bobble,
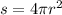
So, the rate of increase of surface area =
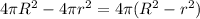
The percentage change in the surface area
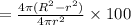
By using equation (i)
The percentage change in the surface area =
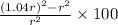

=8.160%
Therefore, the percentage change in the surface area is 8.160%
(b) The volume of the sphere =

So, the change in the volume =
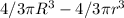
Percentage change in the volume =
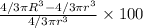
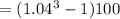 [by using equation (i)]
[by using equation (i)]
=12.486%
Therefore, the percentage change in the volume is 12.486%.