Answer:
Minimum value of
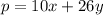 is 80 at (1.5,2.5)
is 80 at (1.5,2.5)
Explanation:
We are given
The objective function is, Minimize
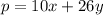
With the constraints as,
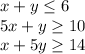
So, upon plotting the constraints, we see that,
The boundary points of the solution region are,
(1,5), (1.5,2.5) and (4,2).
So, the minimum values at these points are,
Points
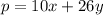
(1,5)
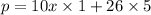 i.e. p = 140
i.e. p = 140
(1.5,2.5)
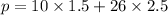 i.e. p= 80
i.e. p= 80
(4,2)
 i.e. p = 92
i.e. p = 92
Thus, the minimum value of
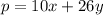 is 80 at (1.5,2.5).
is 80 at (1.5,2.5).