Answer:
Measures of the angles are 20°, 65° and 95°.
Explanation:
We are given that,
Ratio of the angles of the triangle ABC is 4 : 13 : 19.
Let the constant corresponding to the measures of the angle = x.
So, the measures of the angles will be,
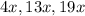
Since, the sum of measures of the angles of a triangle is 180°.
We get,
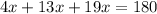
i.e.
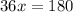
i.e. x = 5
Thus, the measures of the angles are,
4x = 4×5 = 20°
13x = 13×5 = 65°
19x = 19×5 = 95°
Also, sum of the obtained measures = 20° + 65° + 95° = 180°.
Hence, the measures of the angles are 20°, 65° and 95°.