Question

A restaurant serves custom-made omelets, where guests select meat, cheese, and vegetables to be added to their omelet. There are 6 vegetables available, and guests may select any 2 vegetables for their omelet. How many different combinations of 2 vegetables are possible?

from were get the 5 and 4

Answer 1

15 possible combinations

Explanation:

Given

`Vegetables = 6`

`Selection = 2`

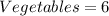
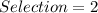
Required

Determine the possible number of combinations

The question emphasizes on "selection" which means "combination".

So; To answer this question, we apply the following combination formula:

`^nC_r = (n!)/((n-r)r!)`

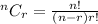
In this case:

`n = 6`

`r = 2`

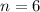
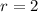
The formula becomes:

`^6C_2 = (6!)/((6-2)!2!)`

`^6C_2 = (6!)/(4!2!)`

`^6C_2 = (6*5*4!)/(4!2*1)`

`^6C_2 = (6*5)/(2)`

`^6C_2 = (30)/(2)`

`^6C_2 = 15`

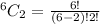
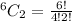
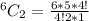
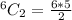
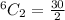
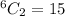
Hence, there are 15 possible combinations