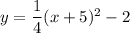Answer:
The equation of parabola:
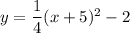
Explanation:
The focus of a parabola is (−5,−1) and the directrix is y=−3
Focus and Directrix are equi-distance from vertex.
Directrix: y=-3 and Focus: (−5,−1)
Thus, The Vertex: (−5,−2)
Equation of parabola:

Distance between Focus and Vertex (p) = 1
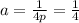
Substitute vertex and value of a into formula
Hence, The equation of parabola: