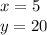Question

The equation of a line is 2/5x+1/10y=2
The x-intercept of the line is and it’s y-intercept is

Answer 1

x intercept is 5

y intercept is 20

Explanation:

When a line intersects the x axis, the y coordinate is zero. therefore we substitute y with zero to get the following equation.

2/5x+ 1/10(0)= 2

solving the equation,

2/5x=2

x=2×5/2

Thus x=5

x intercept is therefore 5

When a line intersects the y axis, the x coordinate is zero

To get the y intercept we substitute x with zero.

2/5(0)+1/10y=2

solving the equation,

1/10y=2

y=2×10/1

y=20

Answer 2

For this case we have the following equation of a line:

`\frac {2} {5} x + \frac {1} {10} y = 2`

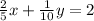
To find the point of intersection with the x axis, we make y = 0:

`\frac {2} {5} x + \frac {1} {10} (0) = 2\\\frac {2} {5} x = 2`

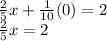
We clear the value of "x":

`x = \frac {2 * 5} {2}\\x = 5`

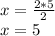
So, the x-intercept of the line is 5.

To find the point of intersection with the y axis, we make x = 0:

`\frac {2} {5} (0) + \frac {1} {10} y = 2\\\frac {1} {10} y = 2`

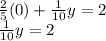
We clear the value of "and":

`y = \frac {10 * 2} {1}\\y = 20`

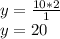
So, the y-intercept of the line is 20.

Answer:

`x = 5\\y = 20`