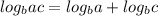Explanation:
Since the question has already been answered, I'd like to add something new, and explain why:
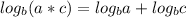
So let's just say that:
 and that
and that
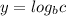
This means that:
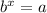 and that
and that
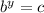 .
.
So if we were to multiply the two, a and c. You get
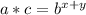
This is due to the exponent identity that:
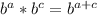
So if you rewrite this in logarithmic form you get:
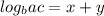
and remember what x and y are equal to? that's right, it's the logarithms
so now you substitute the logarithms back in and get