Answer:
2-2i
Explanation:
So you have the equation:
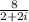
and when you have these equations, you want to get rid of the i, and to do that the simplest way is to square it right? If you simply multiply by 2+2i, you're going to get some i in the middle, so to make sure it's eliminated, you use the difference of squares identity:
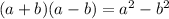 . So you multiply by the conjugate, since it's 2+2i, you multiply by 2-2i, that way it evaluates to 2^2-(2i)^2
. So you multiply by the conjugate, since it's 2+2i, you multiply by 2-2i, that way it evaluates to 2^2-(2i)^2
Multiply both sides by the conjugate of 2+2i
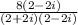
Simplify:
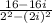
Distribute square the values below
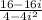
Rewrite the i^2 as -1, since sqrt(-1) = i
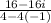
Cancel out the negatives
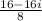
Distribute the division
