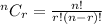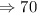Question

What is the coeffieent of (x^4)(y^4) in the expansion of (x+y)^8?

Answer 1

70 is the required coefficient.

Explanation:

We have been given
`(x+y)^8`

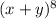
Using the general formula which is:

`(x+y)^n=^nC_(0)x^n\cdot y^0+^nC_(1)x^(n-1)y^1+^nC_[2}x^(n-2)y^2+........+^nC_(n)x^0y^n`

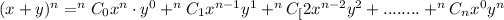
Here, n=8 now, substituting the values in the formula we get:

`(x+y)^8=^8C_(0)x^8y^0+^8C_(1)x^7y^1+^8C_(2)x^6y^2+^8C_(3)x^5y^3+^8C_(4)x^4y^4+....`

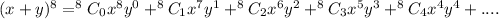
So, we want coefficient of
`x^4y^4`

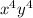
Coefficient is multiple with the term we need to find coefficient of.

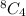`^8C_(4)` is coefficient of
`x^4y^4`

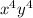
Using
`^nC_(r)=(n!)/(r!(n-r)!)`

`^8C_(4)=(8!)/(4!(8-4)!)`

`\Rightarrow 70`