Answer:
PartA.
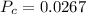
PartB.

Explanation:
To answer this question we must find the area of the square and the area of the circle.
The area of the circle is:
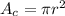
Where r is the radius, and: r = diameter/2 and the diameter = 4
So:
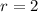
Therefore the area
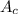 of the circle is:
of the circle is:
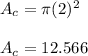
Then, the area of the square is:


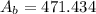
Part A
The probability
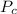 that the dart falls within the black circle is:
that the dart falls within the black circle is:
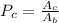
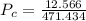
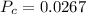
The probability is much closer to 0 than to 1
Part B.
The probability
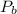 that the dart falls within the white area is:
that the dart falls within the white area is:
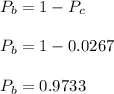
The probability is much closer to 1 than to 0. This is because the area of the black circle is much smaller than the white area, therefore it is more difficult for the dart to hit the black circle.