Question

In any function, f(x) = a(x-h)n + k , a negative leading coefficient means the graph is reflected. True or False

Answer 1

True

Explanation:

For any function of the form
`f(x) = a(x-h) ^ n + k` the coefficient a produces a reflection of the function whenever
`a <0`.

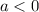We can verify it in the following way.

Take, for example, the function:

`f(x) = 2(x-1) ^ 3`

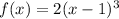
Now let's make
`f(2)`

`f(2) = 2(2-1)^3\\\\f(2) = 2`

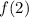
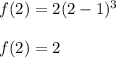
Now let's
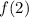`f(2)` in the following function:

`f(x) = -2(x-1)^3`

We have:

`f(2) = -2(2-1)^3\\\\f(2) = -2`

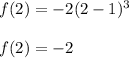
We can see then that the function was reflected in the axis -y by placing a negative coefficient a.

You can see more examples in the attached images

Therefore we can conclude that the statement is true.